平成28年4月1アマの無線工学から、めんどくさそうな問題を抜粋
*******************************************************************************************
A-2
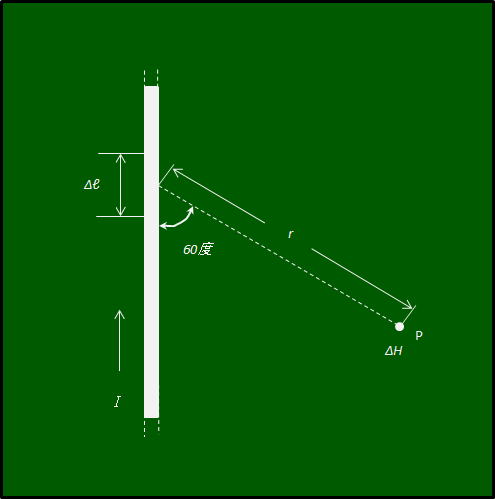
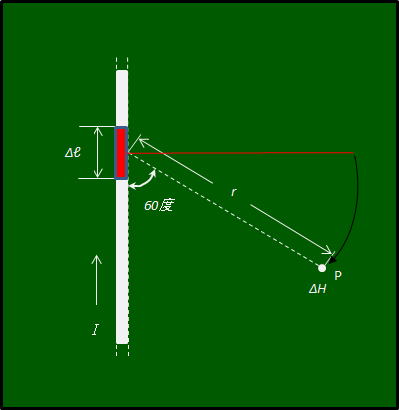
図に示すように、直流電流I [A]が流れている直線導線の微小部分Δℓ [m] から 60度の方向で r [m]の距離にある点Pに、Δℓ によって生ずる磁界の強さΔH [A/m]を表す式として、正しいものを下の番号から選べ。
上級ハムの国試問題をうだうだ解くコーナー 第8弾
平成28年4月1アマの無線工学から、めんどくさそうな問題を抜粋 ![]()
*******************************************************************************************
A-2
図に示すように、直流電流I [A]が流れている直線導線の微小部分Δℓ [m] から 60度の方向で r [m]の距離にある点Pに、Δℓ によって生ずる磁界の強さΔH [A/m]を表す式として、正しいものを下の番号から選べ。
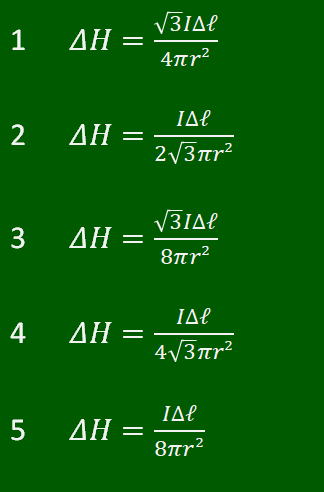 |
 |
よく出題される問題です。
直流電流Ⅰが流れていて、直線導線の微小部分Δℓ [m]のところからのみ磁界が出ているとして、
そこから60度方向 r [m]の p 地点の磁界の強さΔH [A/m]は、どの式で表されるか?
何でわざわざ問いの文章を言い換えたかと言うと、点 p からⅠの流れる線に垂直に下したところからだって電流が流れていれば磁界が出ているだろうに?・・・1図
1図
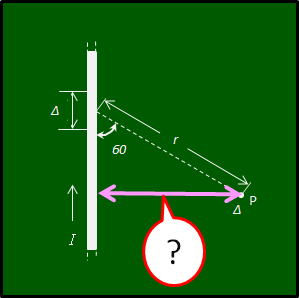
そういう屁理屈を考えると、この問題は解けなくなるので、黄色の「微小部分」と赤の「のみ」を勝手につけ加えて、
自ら納得させます。
ビオ・サバールの法則
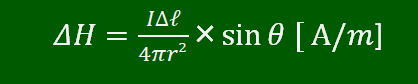
まず、この式を知っていないと、解けません。
それぞれの単位が何を表しているかは問題に書いてあります。
丸暗記すればすむことですが、あえて何でこの式が成立するのかを考えていきたいと思います。
直流電流I [A]と直線導線Δℓ [m]の積によって磁界が放射状に発生しているとして r [m] 離れた一点の強さをまず求めたいので、磁界の発生源を中心としている(半径rの)球の表面積(4πr²)で割り、さらに p点が導線の垂線から何度傾いた位置にあるかで強さが sinθ分だけ弱まる。(あとで気が付きますが、 p点が導線に対し垂直の位置だったら sin 90 °は 1 なので、上の式の sinθは不要です。 でも残念ながら 60°です)
よって磁界の大きさは電流の大きさ、導線の長さ、導線からの測定位置によって変わってきます。
ビオ・サバールの法則は以上の説明を式にしたものです。
その前に「アンペアの法則」とか「右ネジの法則」 とか覚えていますか?
お堅い定義はさておいて、以下のこともおさらいしておきましょう。
下の2図A、中心は導線の断面、手前から向こうに直流電流が流れている時の周りにできる磁力線の方向で、
2図Bは向こうから手前に直流電流が流れている時の周りにできる磁力線の方向です。
余談ですが、ビオ・サバールの法則では磁界の右回り、左回りは考えなくてもよいです。
2図A |
 2図B 2図B |
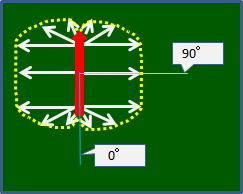
3図のように導線が矢印に沿って続いている間は垂直方向に対して磁界の強さは等しく、
導線から遠くなるにしたがって一律に弱くなる。
しかし赤線(問題ではΔℓ の部分) の左右隅より外側で導線が途切れていると、導線の端の磁界は角度が90度より小さくなるにしたがって弱くなる。導線に対し垂直つまり 90°を 1 とすると、 導線に対し水平で 0 になります。もちろん、
中途半端な角度もあるわけで、それを三角関数で表すと sinθになります。
3図
問題にからませると、(4図)Δℓ の導線に対し、垂直(90度)方向が最も強く、これを 1 とします。角度が低くなるにしたがって1よりも小さくなり、導線に対し水平で 0 (ゼロ)。問題の
P地点 は60度の位置です。
4図
5図
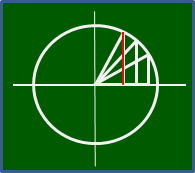
sin60°って何? ・・・イメージは5図の赤線の大きさです。
<ここでまた脱線です>
三角関数のsinθについて、
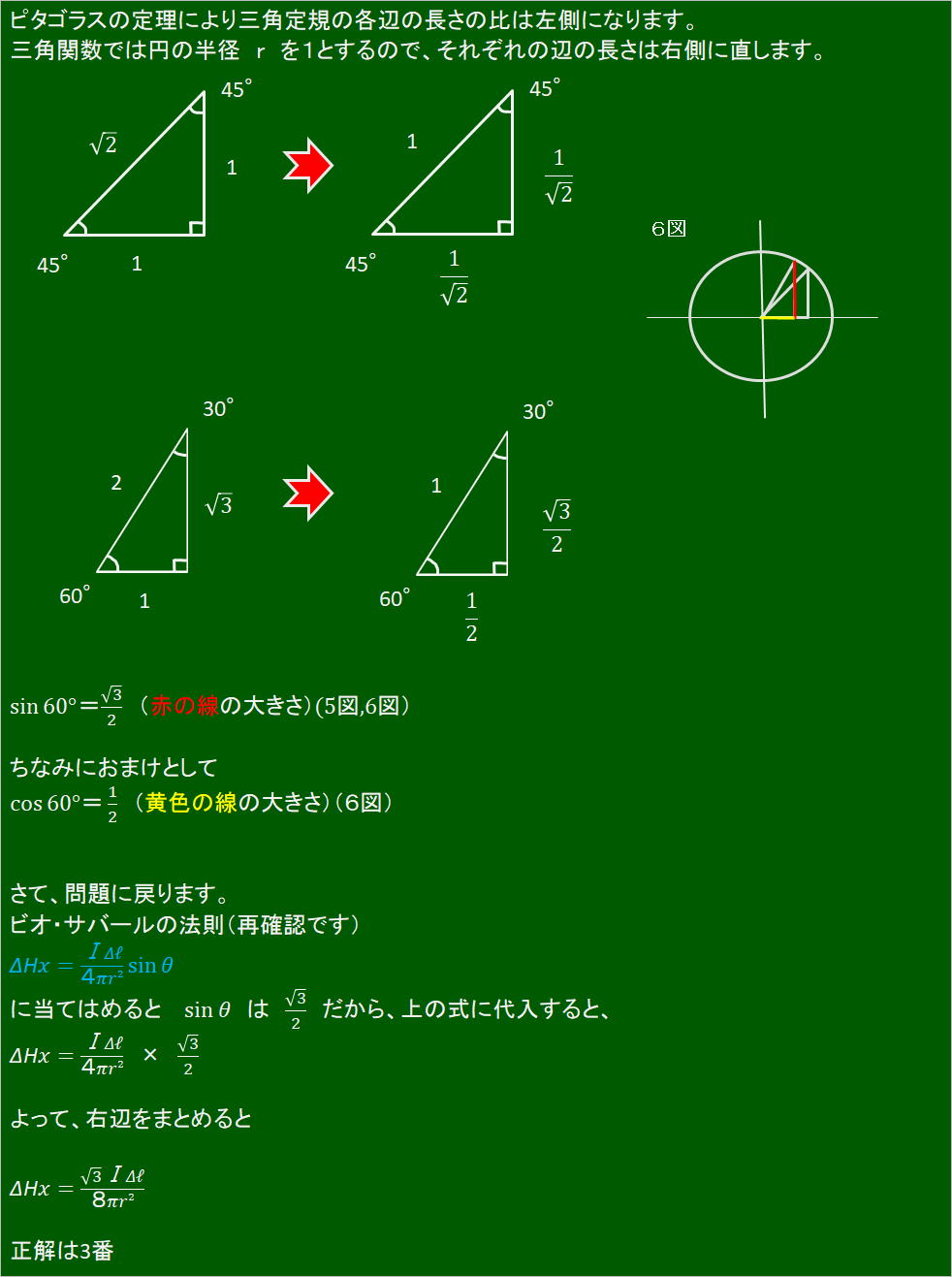
ビオ・サバールの法則の式と三角関数さえ知っていれば、簡単に解くことができますが、使わないとこのような式はすぐに忘れてしまいます。
このページのTOPに戻る