平成28年4月2アマの無線工学から、めんどくさそうな問題を抜粋
*******************************************************************************************
A-5
上級ハムの国試問題をうだうだ解くコーナー 第19弾
平成28年4月2アマの無線工学から、めんどくさそうな問題を抜粋 ![]()
*******************************************************************************************
A-5
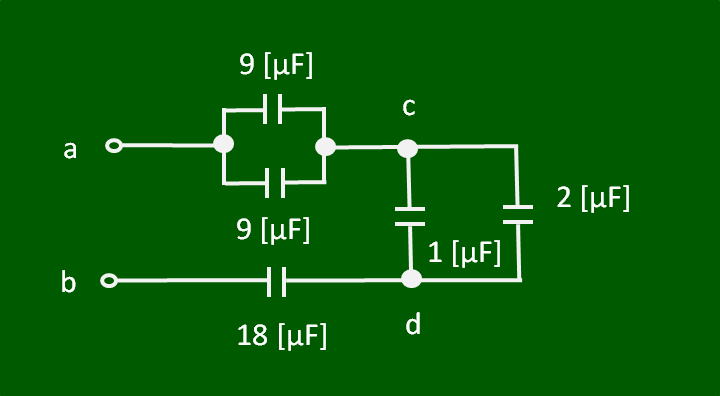
図に示す回路において、端子ab間の電圧が40 [V]であるとき、端子cd間の電圧の値として、正しいものを下の番号から選べ、ただし、電圧を加える前の各コンデンサに蓄えられている電荷の量は、零とする。
|
1 5 [V] 2 8 [V] 3 15 [V] 4 30 [V] |
 |
| この問題を解くには以下の①の式と②、③の計算の仕方が分かっていることです。 Q = C V ・・・・・・➀ 静電容量 C [F]ファラッド のコンデンサの2枚の電極板にV [V] ボルトの電圧を加えると Q [C] クーロンの電荷が蓄えられる。たとえば1[F]のコンデンサに1[V]加えると1[C]の電荷が蓄えられる。 コンデンサの合成容量の求め方
これだけ分かっていても計算できますが、①をさらに掘り下げます。 コンデンサの直列、並列接続。 (2μFのコンデンサを大きく描いてみました) 図1
図1の様な直列と並列のコンデンサの両端に1Vの直流電圧を掛けたら、どうなるか?
合成容量 直列 2/3μF 並列 3μF
電荷 直列 2/3μC 並列 3μC
それぞれにかかる電圧 直列 2μFには1/3V 1μFには2/3V 並列 2μF、1μF 共に1V
それぞれに貯まる電荷 直列 2μF、1μF 共に2/3μC 並列 2μFには2μC 1μFには1μC
そこで、素朴な疑問 、 直列のコンデンサの両端で 2/3μC で 2μF、1μF 共に2/3μC なら、両端は 2/3μC×2 で 4/3μC になるのではないか?・・・とつい考えてしまう。 なりません!
2/3μC です。 直列につないで直流電圧を掛けると各コンデンサの前後は容量に見合った電圧に自然調整して一律に同じ電気量(同じ電荷量)になろうとします。 Q=CV の関係は変わらない。図2参照
それが理解できたところで問題を解きます。
赤枠内の合成容量は 9 [μF] + 9 [μF] = 18 [μF] 黄枠内の合成容量は 1 [μF] + 2 [μF] = 3 [μF] |
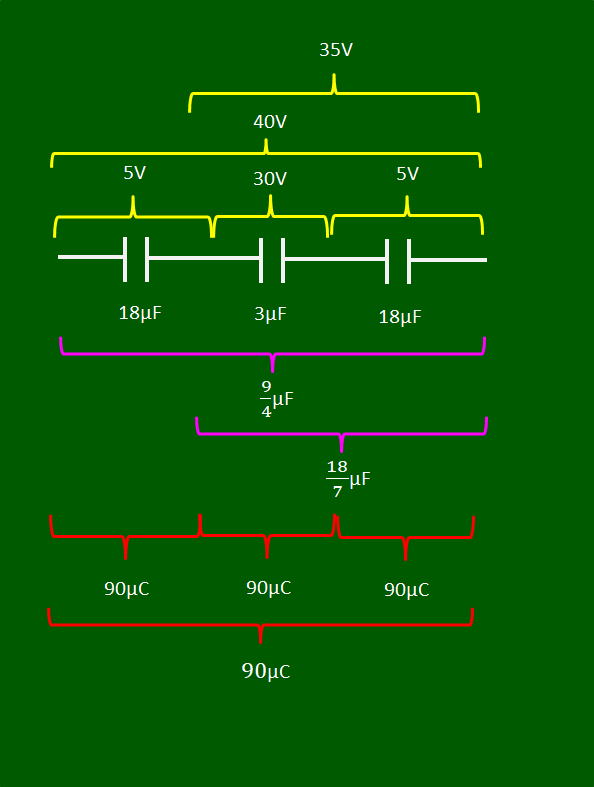
図4は問題の各コンデンサーに掛かる電圧、合成容量、電荷の量の関係です。
この問題のポイントは直列のコンデンサに電圧をかけた場合
各コンデンサに蓄えられる電荷は一律になり Q=CV を満たすように各コンデンサにかかる電圧が自然調整されることが分かっているかです。
図4
 |
このページのTOPに戻る